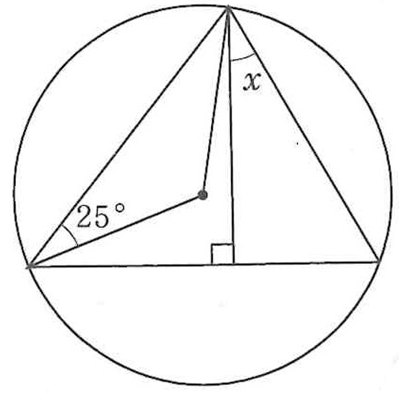
先日2月24日(木)に、令和4年度埼玉県公立入試が実施されました。
受験生の皆さん、本当にお疲れ様でした!
手応えはいかがだったでしょうか?
勝負事である以上、悔しい結果となってしまう方もいることは仕方ありませんが、大事なことは自分の実力を発揮し切れたかどうかです。
『自分は持てる力を最大限に発揮できたはず。』
『あの日、あれ以上自分にできることはないと思うくらい全力を出してきた。』
と思えているのなら、あとは祈りましょう!!
結果は神のみぞ知る。
私も合格発表まで落ち着かない日が続くと思いますが、強い気持ちで生徒達の合格を祈ろうと思います!
さて、そんな今年の問題傾向ですが、学校選択問題の数学で、かなり難易度の高い問題が出題されましたね。
スイカを切るという可愛らしい問題ですが、数学的にはかなり深い問題でした。
下図のように、足りない部分を補って三角錐を作り、体積比を用いて計算していく問題でしたが、時間が限られた試験の中でこの考え方が瞬時に頭に浮かんだ受験生は少なかったと思います。
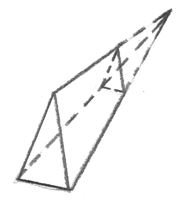
数学の後にはまだ社会・理科・英語の3科目が残されているため、数学での焦りを後の3科目に引きずってしまわなかったかが分かれ道になったように感じます。
このような精神的な部分は、どれだけ早く受験生としての意識を持てたかによっても変わってきます。
中学2年生の皆さん!
皆さんはちょうど1年後、今の先輩達と同じように、公立入試を終えている状態です。
1年という時間は皆さんが思っている以上にあっという間です。
受験勉強にフライングなんてものはありません。
是非、今この瞬間から受験生としての意識を持ち始めましょう!!
教務主任 齊藤 匡寿