皆さん、こんにちは(^^
突然ですが、問題です!
次の問題に答えてみてください!
【問題】△ABCはAB=ACの直角二等辺三角形である。頂点Aから辺BCへ垂線をおろし、その交点をDとする。辺BC、辺ADの長さがそれぞれ10cm、6cmであるとき、△ABCの面積を求めよ。

…
…
…
どうでしょうか?
ちなみにこの問題は、Microsoftの入社試験で出題された問題を少し簡単にしたものなのですが、答えはなんと『このような三角形は存在しない』なのです。
下図の通り、直角二等辺三角形は2つ組み合わせると正方形になるので、対角線の長さは等しくなるはずです。つまり、辺ADの長さは5cmとならなければいけないのです。

さて、皆さんはこの問題の正解を聞いたとき、どう思いましたか?
中には、『こんなのひっかけ問題だ!』と感じた人もいるかもしれませんね。
でも、この問題に対して『ひっかけ問題』という考えをもつ人は日本人に非常に多く、海外では比較的少ないそうです。
では、なぜ海外では『ひっかけ問題』と思う人が少ないのか。
それは、1つの問題を様々な角度から見て考える事を子供のころから教わり、経験しているからです。
このような考え方をクリティカルシンキングと言います。
IT技術が発展し、様々な情報を容易に検索し入手できる昨今では、社会で求められる力の1つであることは間違いありませんね。
しかし、この考え方は普段の数学の勉強や定期テストにも役立てることができます。
例えば、次のような角度を求める問題で考えてみましょう。
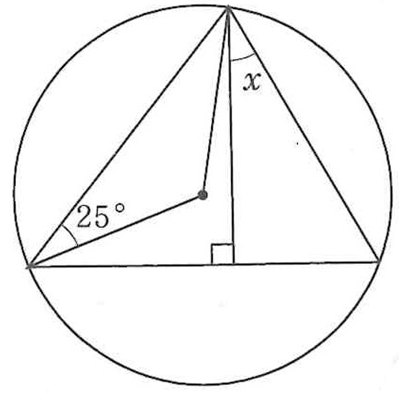
円周角の定理を用いる問題ですが、ここで∠xの大きさを求めた際に、82°という答えが出たとしましょう。
しかし、この∠xをよく見てみると、どう考えても90°の半分以下。つまり45°以下の大きさであることが分かります。
『計算』という1つの方向に集中し過ぎてしまうと、意外とこのようなミスに気づけない場合もあるのですが、『図形』という別の方向からも見てみると、案外簡単に自分のケアレスミスに気付けるはずです。
そう!
皆さんの最も身近なところでは、このケアレスミスの改善にクリティカルシンキングが役立ちます!
是非、数学の家庭学習にこの考え方を取り入れてみてください!
教務主任 齊藤 匡寿
